平面面积算法及应用

平面面积、形心、函数分布积分等问题是C++工程开发中常见问题，下面以平面面积为例介绍此类问题的计算方法；

数学表达

对于平面问题，由格林公式：

$\begin{aligned} & \iint_{D} ({\frac {\partial f_y} {\partial x}} - {\frac {\partial f_x} {\partial y}})\mathrm{d} x \mathrm{d} y = \oint_{\partial D} f_x \mathrm{d} x + f_y \mathrm{d} y \\ where : & \\ & \vec{f} = (f_x, f_y)^T \\ \end{aligned}$

若构造：

$\vec{f}(x,y)= (0, x)^T$

则：

${\frac {\partial f_y} {\partial x}} - {\frac {\partial f_x} {\partial y}} = 1$

可得平面图形面积：

$A = \iint_{D} \mathrm{d} x \mathrm{d} y = \oint_{\partial D} x \mathrm{d} y$

算法描述

若在平面图形边界上将点取得足够密，则可用多边形逼近原平面图形面积，即每段曲线积分使用直线段代替：

$A = \oint_{\partial D} x \mathrm{d} y \approx \sum_{i=0}^{n-1} （\int_{L_i} x \mathrm{d} y）$

而：

$\begin{aligned}\sum_{i=0}^{n-1} （\int_{L_i} x \mathrm{d} y） & = \sum_{i=0}^{n-1} \widetilde{x}_i \Delta y_i= \sum_{i=0}^{n-1} x_{i+\frac 1 2} \Delta y_i \\& = \sum_{k=0}^{n-1} \frac 1 2 (x_{k} + x_{k+1}) (y_{k+1} - y_{k}) \\& = \sum_{k=0}^{n-1} \frac 1 2 (x_{k} y_{k+1} - x_{k+1} y_{k} + x_{k+1} y_{k+1} - x_{k} y_{k}) \\& = \sum_{k=0}^{n-1} \frac 1 2 (x_{k} y_{k+1} - x_{k+1} y_{k}) + \sum_{k=0}^{n-1} \frac 1 2 (x_{k+1} y_{k+1} - x_{k} y_{k}) \\\end{aligned}$

由于封闭图形首尾相连，即：

$x_n = x_0, \qquad y_n = y_0$

故：

$\sum_{k=0}^{n-1} \frac 1 2 (x_{k+1} y_{k+1} - x_{k} y_{k}) = 0$

因此，平面面积算法为：

$A \approx \sum_{i=0}^{n-1} （\int_{L_i} x \mathrm{d} y）= \sum_{k=0}^{n-1} \frac 1 2 (x_{k} y_{k+1} - x_{k+1} y_{k})$

几何意义

上述算法的几何意义是：

$多边形的面积 = \sum_i 多边形每一小段的两端点与原点围成的三角形有向面积$

其图示如下：

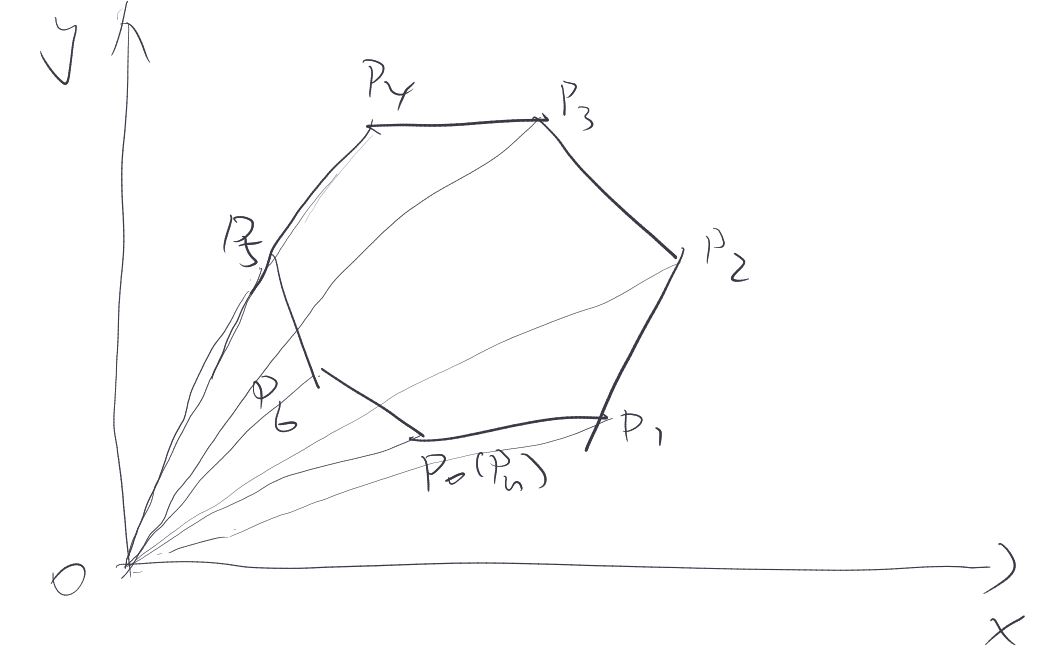
图中，每一个小三角形有向面积的计算方法为：

$A_{k} = \frac 1 2 (\vec{r}_k \times \vec{r}_{k+1}) \cdot \vec{n_z} = \frac 1 2 (x_{k} y_{k+1} - x_{k+1} y_{k})$

核心代码

上述算法的核心代码段如下所示：

double Polygon::area(const std::vector<Point> & pnts)
{
    if (!isPolygon(pnts) || !isAntiClockwise(pnts)) {
        throw std::runtime_error("points must be Polygon and AntiClockwise !");
    }

    double A = 0.0;
    for (size_t i = 0; i < pnts.size(); ++i) {
        A += 0.5 * (pnts[i].x() * pnts[i + 1].y() - pnts[i + 1].x() * pnts[i].y());
    }
    
    return A;
}

拓展推广

1. 此种方法可以求解平面区域分布函数 $g(x, y)$ 的面积分问题，只要构函数 $\vec{f}(x, y)$，使之满足如下条件即可：

${\frac {\partial f_y} {\partial x}} - {\frac {\partial f_x} {\partial y}} = g(x, y)$

2. 与二维问题类似，对于三维问题，使用高斯公式即可将体分布函数 $g(x, y, z)$ 的积分问题转化为闭曲面积分问题，由于本文内容所限，故不在此展开；

参考

• 谢树艺，矢量分析与场论，高等教育出版社，2012年05月；
• 任意多边形的面积公式；

---